Many real world problems can be framed as regression: use a collection of features \(X\) to predict a real-valued quantity \(y\). However, this framing can obfuscate a very important detail: which kinds of mistakes are most important to avoid? Many factors can influence this, including how the predictions will be used, the configuration of existing systems, and the safeguards that are in place.
Despite this variation in objective, most commonly used regression metrics weight extremely large mistakes much more harshly than several somewhat large mistakes or many medium mistakes.
- Mean Square Error \(MSE(\mathbf{X}, \mathbf{y}) = avg (f(X_i) - y_i)^2\) and its normalized variant R-Squared weigh large mistakes dramatically larger than small ones, and it is quite common for model \(f_1\) to have a better MSE and R-Squared than model \(f_2\), but to generate worse predictions on 95% of cases.
- Mean Absolute Error \(MAE(\mathbf{X}, \mathbf{y}) = avg \vert f(X_i) - y_i \vert\) is less sensitive to large mistakes than MSE, but still quite sensitive to outliers. MAE behaves similarly to MSE when errors are distributed logarithmically (e.g. price changes).
- Pearson correlation \(Corr(\mathbf{X}, \mathbf{y}) = \frac{Cov(f(X),y)}{\sqrt{var(f(X))var(y)}}\) is similarly sensitive to large mistakes as MSE.
- Spearman correlation (ordinal transformed Pearson correlation) is very sensitive to certain kinds of large mistakes, such as large overestimates on the smallest values of \(y_i\).
This sensitivity to large mistakes is sometimes appropriate. Consider a high frequency trading system that estimates the potential return of different strategies and executes the optimal strategy automatically. A single massive mistake can bankrupt the trading firm, so it is critical that this never happens.
However, consider instead a system that external users query for informational purposes (like the Zestimate). It is more important that this system generates reasonably good predictions 99% of the time than that it never makes a massive mistake. Any user who receives an estimate that they perceive as “obviously wrong” will stop using the system, so once a mistake is past this boundary its magnitude becomes irrelevant. A successful system will therefore minimize the number of users who end up in this bucket, rather than weighting some mistakes in this bucket higher than others. We can capture this kind of mistake dynamics with percentile error metrics like P50 and P95.
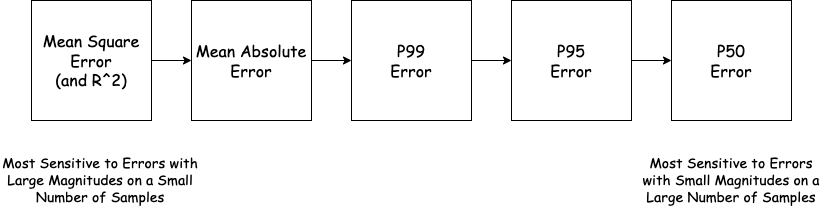
For example, the P95 error is the smallest value such that for 95% of pairs \((X_i, y_i)\) the quantity \(\vert f(X_i) - y_i \vert\) is smaller than this value. The magnitude of the worst 5% of errors has no impact on the P95 error. Similarly, the p50 error (aka the median error) is useful for tracking performance across many samples in the dataset. Any large improvement to the P50 error usually represents improvements on a large number of samples. Contrast this to MSE or correlation which can swing even when the prediction only changes on a single sample.