A common problem in machine learning is “use this function defined over this small set to generate predictions over that larger set.” Extrapolation, interpolation, statistical inference and forecasting all reduce to this problem. The Kan extension is a powerful tool in category theory that generalizes this notion.
In a recent paper I explored how we can apply this idea across supervised and unsupervised learning applications. In this paper we cast basic machine learning problems in category theoretic language, apply the Kan extension, translate the result back to machine learning language, and study the behavior of the resulting algorithms.
The Kan Classifiers
This blog post dives deeper into the first application described in that paper. There is no category theory required, and you don’t need to read the paper to understand this post.
Suppose we have a set of training samples \(\{(X_1, y_1), (X_2, y_2), \cdots\}\) where each \(X_i\) is a sample from the set \(S\). For example, \(S\) might be \(R^n\) if we have \(n\) continuous features. Now suppose that for some preorder \(S'\) we derive a transformation \(f: S \rightarrow S'\) such that when \(f(X_i) \leq_{S} f(X_j)\) we tend to see that \(y_i \leq_{S} y_j\).
If we apply this transformation to our training dataset \(\{(f(X_1), y_1), (f(X_2), y_2), \cdots\}\) there are two ways we could use the resulting ordered list to generate a prediction on a new sample \(f(X_j)\).
- Predict \(y_j\) to be the largest label across all training samples which are ordered below this new sample. We call this the left Kan classifier.
- Predict \(y_j\) to be the smallest label across all training samples which are ordered above this new sample. We call this the right Kan classifier.
The left Kan classifier has no false negatives and the right Kan classifier has no false positives on the training dataset.
Transformation
In order for the Kan extension to work well we need to learn a transformation \(f: S \rightarrow S'\) of our data such that when \(f(X_i) \leq_{S} f(X_j)\) we tend to see that \(y_i \leq_{S} y_j\). Intuitively, such a transformation will order any collection of points in the feature space as closely as possible to the ordering of those points in the prediction space.
Since the left Kan classifier has no false negatives and the right Kan classifier has no false positives on the training dataset an optimal transformation will minimize the size of the region on which these classifiers disagree.
We can approximate the size of the disagreement region with the ordering loss:
def get_ordering_loss(self, X_true, X_false, training=True):
return tf.reduce_sum(tf.math.maximum(0.0,
tf.math.reduce_max(
tf.transpose(self.predict_tf(X_false, training=training)), axis=1) -
tf.math.reduce_min(
tf.transpose(self.predict_tf(X_true, training=training)), axis=1)))
The ordering loss will only be zero when the transformation perfectly orders the data in the training dataset. See Proposition 3.3 in the paper for more details
Ensemble
Although transforming our data with an ordering loss can improve the performance of our model, it is not enough in practice. Since the left and right Kan extensions must respectively drive false negatives and false positives to zero, these algorithms are very sensitive to outliers. This is a common theme with algorithms that are derived from category theoretic constructs.
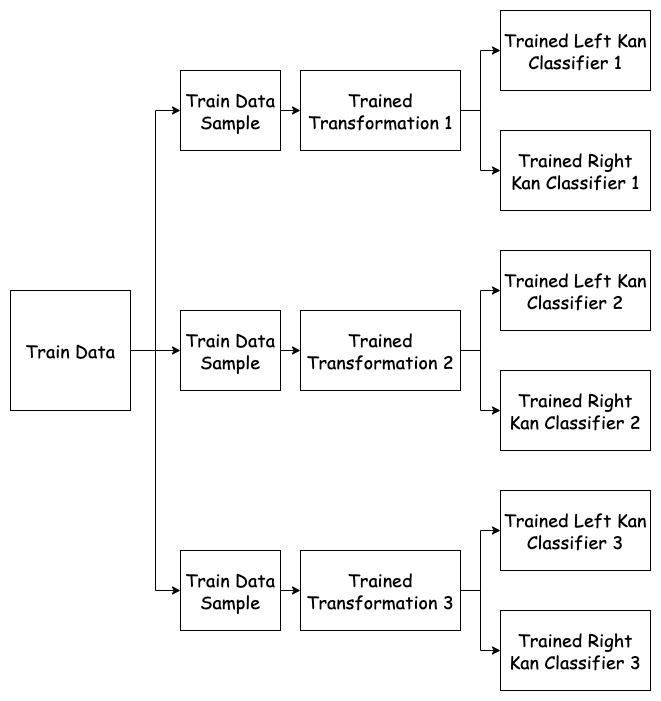
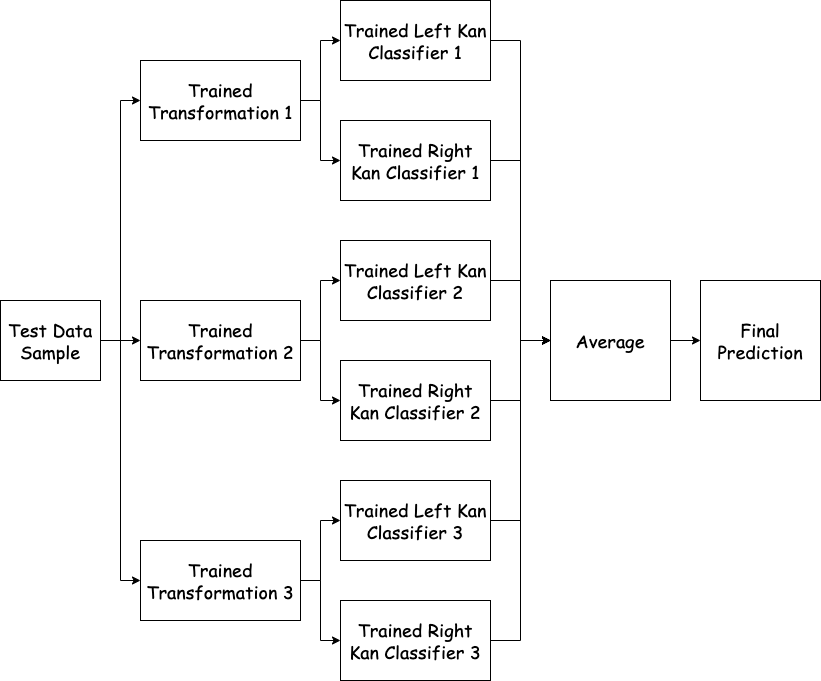
One way to mitigate this issue is to ensemble multiple Kan classifiers together. Explicitly, we can use the Bagging algorithm to repeatedly subsample our data, train a transformation \(f_i: S \rightarrow S_i'\) on this sample, and fit the left and right Kan classifiers as base models on the transformed data in this sample. We can then take the average prediction of the trained classifiers. Since any particular outlier sample will be dropped from most data subsets we expect the ensemble classifier to perform better in practice.
Training the KanEnsembleClassifier
Predicting with the KanEnsembleClassifier
Experiment
Let’s compare how this KanEnsembleClassifier to the scikit-learn RandomForestClassifier on the the Shirt vs T-shirt task from the Fashion MNIST dataset.
We can compare the model performance across different base estimator counts. We see that the KanEnsembleClassifier consistently performs slightly better.
| model | n_estimators | TP rate | TN rate | ROC-AUC |
|---|---|---|---|---|
| RandomForestClassifier | 10 | 0.775 | 0.897 | 0.836 |
| RandomForestClassifier | 50 | 0.807 | 0.905 | 0.856 |
| RandomForestClassifier | 100 | 0.809 | 0.891 | 0.850 |
| RandomForestClassifier | 500 | 0.815 | 0.901 | 0.858 |
| KanEnsembleClassifier | 10 | 0.817 | 0.911 | 0.864 |
| KanEnsembleClassifier | 50 | 0.821 | 0.905 | 0.863 |
| KanEnsembleClassifier | 100 | 0.817 | 0.905 | 0.861 |
| KanEnsembleClassifier | 500 | 0.821 | 0.909 | 0.865 |
You can find the code on github here.